Когда мы анализируем поведение функций, иногда может возникнуть необходимость найти точки, где они прерываются. Эти точки, известные как точки разрыва, играют важную роль в анализе и понимании функциональных графиков. В этом разделе мы исследуем различные подходы и методы, позволяющие нам найти эти точки и понять их значение.
Одним из основных способов обнаружить точки разрыва является анализ производных. При производном анализе мы исследуем изменение функции в различных точках и ищем места, где это изменение не определено или бесконечно. Это может быть связано с неопределенными значениями или скачками в функции, которые вызывают разрывы.
В дополнение к анализу производных, мы также можем использовать графический метод для обнаружения точек разрыва. Представляя функцию в виде графика, мы можем исследовать его форму и структуру, выявляя места, где происходят перебои или несвязности. Графический метод может быть особенно полезен при анализе сложных функций, где производная не является интуитивной или доступной.
Методы и понятия для определения точек разрыва функции

В данном разделе будет рассмотрено несколько методов и важных понятий, которые помогут найти точки разрыва функции. Разрывы в функциях могут возникать по разным причинам, из-за которых график функции может быть прерывистым или неопределенным в некоторых точках. Более детальное изучение данных методов и понятий позволит более точно определить и классифицировать такие точки.
| Метод | Описание |
|---|---|
| Анализ графика | Этот метод основан на изучении формы и поведения графика функции. Путем наблюдения за графиком в окрестности подозрительных точек, можно определить наличие разрывов и их тип: разрыв первого рода, разрывы второго рода или разрывы третьего рода. |
| Использование пределов | Для некоторых явных и неявных функций можно вычислить пределы в подозрительных точках. Если предел существует и конечен, то в данной точке функция может быть непрерывной. Если пределы различны для разных сторон точки, это может указывать на наличие скачков или разрывов. |
| Исследование алгебраической формулы | Для некоторых функций можно провести математические преобразования, чтобы упростить формулу и выделить особые значения аргумента, при которых функция может быть неопределенной. Проведение таких преобразований помогает определить точки разрыва. |
| Изучение производной | Изучение производной функции позволяет найти места, где она не является дифференцируемой, что может указывать на наличие разрыва функции. Различные типы разрывов могут иметь свои особенности в поведении производной в этих точках. |
Усвоение этих методов и понятий поможет более точно и систематически исследовать функции и находить их точки разрыва. Применение этих знаний в решении задач позволяет проводить анализ функций с точки зрения их разрывов и определять характер и типы этих разрывов.
Значение точки разрыва функции и ее существенность

Значение точек разрыва в анализе функций
Точки разрыва достаточно важны в анализе функций, поскольку они позволяют определить границы поведения функции в конкретной области определения. Они могут указывать на смену значений функции, нарушение непрерывности или возникновение положительных или отрицательных бесконечностей. Поэтому понимание и определение точек разрыва имеет большое значение для понимания свойств и характеристик функций.
Импортантность изучения точек разрыва
Изучение точек разрыва функции является важной задачей в математике и её различных приложениях. Оно помогает нам понять, как функция ведет себя в разных областях определения и выявить особенности ее поведения вблизи таких точек. Анализ точек разрыва функции также может быть полезен при построении графиков и определении математических моделей для конкретных физических явлений и процессов.
Поэтому учет и изучение точек разрыва функции является необходимым для получения более глубокого понимания ее поведения и свойств.
Типы точек разрыва функции: открытый, закрытый и устранимый

В ходе изучения точек разрыва функции, становится очевидно, что не все разрывы одинаковы. В зависимости от характера и поведения функции вблизи точки, разрывы делятся на три типа: открытые, закрытые и устранимые.
Открытые точки разрыва похожи на границу между двумя разными функциями. В таких точках график функции имеет две отдельные ветви, не сходящиеся в одну точку. Одна ветвь может стремиться к бесконечности, а другая сохраняться на конечном уровне, либо обе ветви стремятся к бесконечности, но с разными знаками. Например, при делении на ноль.
Закрытые точки разрыва являются более гармоничными с точки зрения взаимодействия функции в окружающих точках. В таких точках график функции имеет две ветви, не стремящиеся к бесконечности, и встречающиеся в определенной точке. Например, при различных определенных значениях переменной.
Устранимые точки разрыва отличаются от предыдущих двух типов тем, что их можно устранить, исправив функцию в данной точке. В таких точках график функции может иметь прерывание, обусловленное, например, некорректно заданным значением функции в точке или отсутствием определения функции в данной точке. Исправляя функцию в этой точке или дополняя определение, можно избавиться от разрыва.
Изучение этих различных типов точек разрыва позволяет лучше понять поведение функции и найти методы для их устранения или решения. При анализе функции, необходимо учитывать эти различия для корректной интерпретации графика и построения математических моделей.
Пример 1: поиск точки разрыва функции с использованием метода анализа предела

Рассмотрим конкретный пример нахождения точки разрыва функции с применением метода анализа предела. В данном разделе мы будем исследовать функцию и определить, в каких точках она имеет разрыв.
| Функция | Предел слева | Предел справа | Точка разрыва |
|---|---|---|---|
| f(x) = 1/x | limx→0- f(x) = -∞ | limx→0+ f(x) = +∞ | x = 0 |
В данном примере рассматривается функция f(x) = 1/x. Для нахождения точки разрыва, мы вычисляем пределы функции слева и справа от возможной разрывной точки. Если значения пределов различны, то функция имеет точку разрыва.
В нашем примере, при анализе предела слева, получаем значение -∞ (минус бесконечность), а при анализе предела справа - +∞ (плюс бесконечность). Таким образом, функция f(x) = 1/x имеет точку разрыва при x = 0.
Использование графика для определения точек разрыва функции

В данном разделе рассмотрим пример использования графика функции для определения точек разрыва. Знание основ графической интерпретации функции поможет нам выявить места, где функция может быть неопределенной или иметь разрывы.
График функции визуально отображает зависимость значений функции от ее аргументов. При анализе графика мы можем обнаружить различные особенности функции, включая ее разрывы. Точками разрыва функции являются те значения аргументов, при которых функция не определена или имеет разрывы в виде отсутствия непрерывности или изменения поведения функции.
На графике точки разрыва функции могут быть представлены пропуском значений на графике, разрывом графика или изменением его направления. Например, у функции может возникать разрыв в точке, где знаменатель выражения обращается в ноль или деление на ноль. Также функция может иметь разрывы при изменении определения функции в различных областях аргументов.
Для определения точек разрыва на графике функции необходимо внимательно изучить его особенности и анализировать значения функции в различных областях аргументов. При обнаружении разрыва следует проводить дополнительный анализ и проверку с помощью математических методов, чтобы убедиться в точности определения разрыва.
Использование графика для определения точек разрыва функции позволяет получить наглядное представление о поведении функции и выявить особенности, которые не всегда могут быть заметны при решении уравнений или использовании других методов анализа. Этот подход является эффективным и позволяет визуально представить и проанализировать разрывы функции.
Эффективный подход к обнаружению переломных точек функции посредством дифференциального анализа
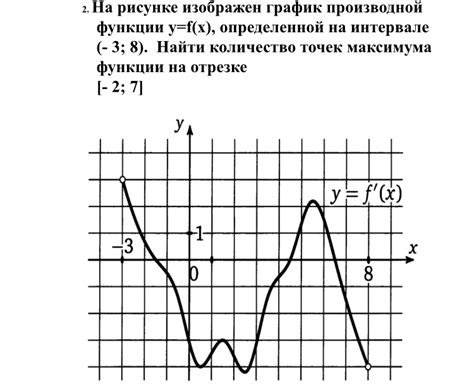
В данном разделе мы рассмотрим эффективный метод определения точек разрыва функции, основанный на дифференциальном анализе. Дифференциальный анализ позволяет изучать свойства функций и их изменения при помощи производных. Используя этот подход, мы сможем исследовать функции на наличие точек разрыва и определить их типы.
В процессе дифференциального анализа мы сосредотачиваемся на анализе производных функций. Первая производная функции позволяет определить точки, в которых функция может иметь разрывы вида разрыва первого рода (характеризующиеся отсутствием пределов). Вторая производная функции дает информацию о точках, в которых функция может иметь разрывы второго рода (характеризующиеся расхождением пределов).
В ходе анализа производных мы обращаем внимание на такие факторы, как положение и знак производных, промежутки возрастания и убывания функции, точки экстремума, а также точки разрыва. При достаточно глубоком анализе этих факторов мы сможем точно определить местоположение и типы точек разрыва функции.
Дифференциальный анализ является мощным инструментом для обнаружения точек разрыва функции, так как он позволяет выявить даже скрытые разрывы, которые могут оказывать существенное влияние на поведение функции в определенных областях. Наш эффективный метод, основанный на дифференциальном анализе, позволит вам систематизировать и упростить процесс обнаружения точек разрыва функции и повысить точность результатов.
Вычисление точек разрыва функции с использованием специальных программ и онлайн-калькуляторов

Существует возможность использовать специализированные программы и онлайн-калькуляторы для вычисления точек разрыва функций. Эти инструменты предоставляют удобный и эффективный способ определения точек разрыва функции без необходимости проведения сложных математических вычислений.
С помощью этих программ и калькуляторов вы можете ввести свою функцию и получить результаты, которые покажут точки разрыва. Это особенно удобно, если у вас нет времени или навыков для ручного решения задачи. Вместо этого, вы можете полагаться на высокотехнологичные программы и онлайн-ресурсы, которые точно и быстро определят точки разрыва вашей функции.
Такие программы и калькуляторы обычно предлагают простой и интуитивно понятный пользовательский интерфейс, где вы можете ввести вашу функцию в виде уравнения или графика. Затем программы произведут расчеты и предоставят вам точки разрыва, возможно с указанием типа разрыва и его характеристик.
Использование специальных программ и онлайн-калькуляторов для вычисления точек разрыва функции обладает несколькими преимуществами. Во-первых, это экономит время и упрощает процесс анализа функций, особенно для сложных и многочленных функций. Во-вторых, вы можете быть уверены в точности результатов, поскольку программы используют точные математические алгоритмы. И, наконец, услуги онлайн-калькуляторов доступны бесплатно и всегда доступны в сети, что делает их удобными для использования в любое время и в любом месте.
- Преимущества вычисления точек разрыва функции специальными программами:
- - Экономит время и упрощает процесс анализа функций
- - Обеспечивает точные результаты с использованием математических алгоритмов
- - Бесплатные онлайн-калькуляторы всегда доступны в сети
Как определить точки разрыва функции, если график функции неизвестен?
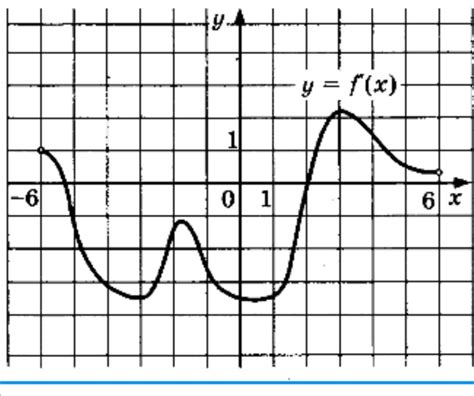
Когда располагаемыми данными о функции мы обладаем, задача по нахождению точек разрыва может быть довольно простой. Но что делать, если мы не знаем графика функции? Как в таком случае определить места, где функция перестает быть непрерывной?
Существует несколько методов, которые позволяют нам определить точки разрыва функции, даже при отсутствии графика. Одним из таких методов является анализ пределов. С помощью вычисления предела функции в определенных точках мы можем определить, находится ли функция непрерывно в этой точке или нет. Если пределы существуют, но не равны друг другу, то это говорит о наличии точки разрыва. Этот метод особенно полезен, когда функция задана формулой, которая допускает вычисление пределов.
Еще одним методом, который поможет определить точки разрыва функции без знания графика, является анализ определения функции. Исследуя определение функции, мы можем обнаружить, что в некоторых точках возникают неопределенности или некорректные значения. Например, если функция содержит деление на ноль или извлечение корня из отрицательного числа в определенных точках, то это указывает на наличие разрыва в этих местах. Таким образом, анализ определения может быть полезным методом для нахождения точек разрыва.
В итоге, хотя знание графика функции облегчает задачу по нахождению точек разрыва, мы можем использовать анализ пределов и определения функции для определения этих точек даже без графика. Эти методы позволяют нам найти места, где функция перестает быть непрерывной и помогают в дальнейшем анализе и изучении свойств функции.
Методы определения исправляемых локальных возмущений функции

В данном разделе мы рассмотрим различные подходы к определению и устранению устранимых точек разрыва функций. Изучение этих методов позволит нам более точно анализировать поведение функций и добиваться их более гладкого и непрерывного характера.
Первым методом, который мы рассмотрим, является анализ графиков функций. График функции позволяет нам визуально оценить наличие устранимых точек разрыва. Мы можем обратить внимание на резкие скачки или разрывы в графике функции, что может указывать на присутствие точек разрыва. Однако данный способ не всегда является точным и требует дополнительной проверки.
Другим методом, который можно использовать для нахождения устранимых точек разрыва функций, является анализ асимптотического поведения функции. Путем вычисления пределов или анализа асимптот графика функции мы можем выявить точки, в которых функция имеет неопределенное поведение или разрывы. Этот метод является более точным и пригодным для формального доказательства наличия точки разрыва.
Дополнительным способом определения устранимых точек разрыва функции является использование алгебраического анализа. Мы можем попытаться упростить выражение функции и проанализировать условия, при которых функция может иметь разрывы. При этом необходимо учесть особенности работы с особыми точками, такими как деление на ноль или логарифмирование отрицательных чисел.
В итоге, комбинируя различные методы анализа, мы сможем более точно определить и исправить устранимые точки разрыва функции. Это позволит нам получить более гладкие и непрерывные функции, обеспечивая более точные результаты и предсказания на практике.
Стандартные принципы выявления точек перегиба функции: исключение ошибок

В данном разделе мы рассмотрим основные принципы, которые помогут избежать ошибок при анализе и выявлении точек разрыва функции. При рассмотрении различных примеров подробно изучим эффективные методы, позволяющие точно определить и классифицировать эти точки.
В первую очередь стоит отметить, что точки перегиба функции имеют особую природу и требуют особого подхода к их выявлению. Необходимо учесть разнообразные факторы, такие как наличие разрыва первого рода, разрыва второго рода или излома функции в области точки разрыва.
Для начала, важно определить, является ли точка разрыва устранимой или неустранимой. Здесь чрезвычайно важно проанализировать пределы функции с обеих сторон точки разрыва и выяснить, сходится ли он или расходится. Это позволит избежать распространенной ошибки и точно определить тип разрыва.
Далее следует обратить внимание на тип точки разрыва, такой как разрыв первого рода или разрыв второго рода. Для этого необходимо изучить поведение функции в окрестности точки разрыва, а также анализировать существование односторонних пределов. Этот анализ поможет установить наличие или отсутствие разрывов в функции и классифицировать их соответственно.
И наконец, необходимо учесть возможность излома функции в области точки разрыва. Это явление может наблюдаться при наличии разрыва второго рода, и для его определения необходимо исследовать поведение функции в левой и правой окрестностях точки разрыва. Анализ данных окрестностей позволит точно определить наличие или отсутствие излома функции и соответствующим образом классифицировать точку разрыва.
Таким образом, использование стандартных принципов и правил разбора точек разрыва функций позволяет избежать ошибок при их выявлении. Подробное анализирование различных примеров с применением эффективных методов обеспечивает точность определения типов и характеристик точек разрыва, что важно для правильного понимания свойств функций и их дальнейшего использования в математических расчетах и приложениях.
Анализ дифференциального уравнения для определения точек разрыва функции

В данном разделе мы рассмотрим подходы к получению точек разрыва функции, основанные на анализе дифференциального уравнения, не используя прямое определение или численные методы. Мы подойдем к изучению разрывов функции с учетом производных и их связи с непрерывностью функций. Это позволит обнаружить и классифицировать точки разрыва, предоставляя более глубокое понимание поведения функций.
Анализ дифференциального уравнения может быть полезным инструментом для выявления точек разрыва функции. Путем производного анализа можно определить места, где функция не определена или имеет разрывы. Также можно провести исследование границы интервалов непрерывности, исследуя знаки производных и их пределы.
Рассмотрим пример функции, для которой необходимо определить точки разрыва через анализ дифференциального уравнения:
Дана функция:
f(x) = |x|
Для анализа точек разрыва произведем дифференцирование данной функции:
f'(x) = sign(x)
Проанализируем производную. Знак производной меняется при x = 0, что указывает на наличие точки разрыва при x = 0. Для классификации точки разрыва дополнительно рассмотрим пределы производной при x → 0- и x → 0+:
lim (x → 0-) f'(x) = -1
lim (x → 0+) f'(x) = 1
Получается, что функция имеет разрыв первого рода в точке x = 0, так как левый и правый пределы производной отличаются.
Анализ дифференциального уравнения позволяет идентифицировать точки разрыва функции, исходя из его свойств и условий задачи. Этот метод позволяет увидеть глубину изменений функций и их связь с производными, открывая новые пути исследования и понимания разрывов функций.
Вопрос-ответ

Какие методы можно использовать для поиска точек разрыва функции?
Для поиска точек разрыва функции можно использовать несколько методов. Один из них - метод анализа графика функции. Для этого нужно построить график функции и исследовать его на наличие разрывов. Другой метод - метод исследования функции. Здесь нужно проанализировать поведение функции вблизи возможных разрывов, например, вычислить лимиты функции в этих точках. Также можно использовать математические формулы или компьютерные программы для нахождения точек разрыва.
Как найти точки разрыва функции с помощью графика?
Для того чтобы найти точки разрыва функции с помощью графика, нужно построить график функции и внимательно его изучить. Разрыв функции может быть виден на графике в виде прерывистого или несвязного участка. Например, если график функции имеет вертикальную асимптоту, то в точке пересечения с осью абсцисс функция будет иметь разрыв. Также стоит обратить внимание на точки излома графика, где функция может иметь разрыв первого рода.
Как найти точку разрыва функции, используя лимиты?
Для нахождения точки разрыва функции с помощью лимитов, нужно вычислить лимиты функции слева и справа от возможной точки разрыва. Если лимиты не совпадают, то функция имеет разрыв в этой точке. Например, если лимит функции при x, стремящемся к некоторому числу c, существует и конечен, но не совпадает с самим значением функции в точке c, то в этой точке будет разрыв первого рода. Если же хотя бы один из лимитов не существует, то функция будет иметь разрыв второго рода в данной точке.