Когда сталкиваешься с задачей доказательства взаимной простоты двух чисел, бывает сложно найти подходящие методы и алгоритмы. Однако, используя логический анализ и изучение взаимной неприводимости, мы можем достичь прозрачного и обоснованного результата. В данной статье мы рассмотрим применение данного подхода на примере чисел 455 и 968.
Логический анализ позволяет выявить общие закономерности и свойства чисел, а также выделить ключевые элементы, которые влияют на взаимную неприводимость. В рамках данной задачи, мы исследуем особенности чисел 455 и 968, применяя методы, основанные на логике и математических принципах.
Взаимное отношение двух чисел и их численное взаимодействие

В данном разделе мы рассмотрим взаимную простоту двух чисел и способы ее доказательства. Мы также исследуем различные методы и алгоритмы, которые можно применить для определения взаимной простоты чисел.
Простота чисел, или отсутствие общих делителей, играет важную роль в различных областях, таких как криптография и теория чисел. Взаимная простота двух чисел означает, что они не имеют общих делителей, кроме единицы. Это свойство позволяет нам выполнять различные операции с числами, такие как нахождение наибольшего общего делителя и решение уравнений.
Существуют разные методы доказательства взаимной простоты чисел. Один из них основан на использовании понятия наибольшего общего делителя (НОД). Другой метод, называемый алгоритмом Евклида, позволяет нам последовательно находить НОД двух чисел и, тем самым, определить их взаимную простоту.
Определение простых чисел
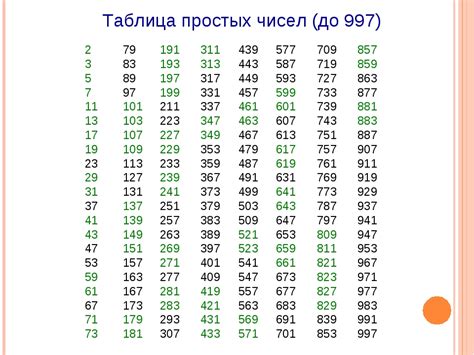
Простые числа не имеют делителей, кроме 1 и самого себя. Они отличаются от составных чисел, которые имеют более одного делителя. Используя теорему Евклида и другие математические концепции, существуют различные методы определения простых чисел.
- Перебор делителей: один из простейших и наивных способов определения простого числа - проверка его на делимость на все числа, меньшие его самого. Если ни одно из этих чисел не делит данное число без остатка, то оно является простым числом.
- Тест Ферма: основывается на малой теореме Ферма и позволяет проверять на простоту числа с помощью случайных чисел и степеней. Используется в таких алгоритмах, как тест Миллера-Рабина.
- Решето Эратосфена: эффективный алгоритм для нахождения всех простых чисел до заданного предела. Простые числа выделяются путем исключения всех их кратных чисел из списка.
- Алгоритмы на основе факторизации: основаны на разложении числа на простые множители. Если число имеет только два множителя - 1 и самого себя, то оно является простым числом.
- Тесты на простоту: существуют различные алгоритмы, проверяющие числа на простоту, используя различные математические теоремы и методы, такие как тест Люка-Лемера для чисел Мерсенна и тест Лукаса-Миллера.
Определение простых чисел имеет большое значение в криптографии, кодировании и других областях, где осуществляется обработка больших чисел и безопасность данных. Понимание основных методов и алгоритмов определения простоты поможет нам глубже понять и использовать эти числа в практических задачах.
Метод проверки на простоту

| Метод | Описание |
|---|---|
| Перебор делителей | Этот метод предполагает перебор всех возможных делителей числа и определение, делится ли число нацело на каждый из них. Если в результате перебора не найдено делителей, отличных от 1 и самого числа, тогда число считается простым. |
| Тест Миллера-Рабина | Данный тест основан на применении модульной арифметики и вероятностном подходе. Он позволяет верифицировать простоту числа с заданной вероятностью ошибки. |
| Тест Лукаса-Лемера | Этот метод, применяемый для проверки простоты чисел Ферма, используется вместе с алгоритмом возведения в степень по модулю. Он основан на свойствах итерационных последовательностей. |
Упомянутые методы представляют собой лишь небольшую часть доступных алгоритмов для проверки чисел на простоту. Использование различных алгоритмов с разными подходами позволяет увеличить точность проверки и учесть различные особенности чисел. Применение этих методов позволит нам определить простоту чисел 455 и 968.
Расчет наибольшего общего делителя (НОД) двух чисел

Для расчета НОД двух чисел будут использованы алгоритмы и методы, которые основаны на различных математических концепциях. Данный раздел будет описывать основные шаги этих алгоритмов, а именно:
| Шаг 1: | Определение наименьшего числа из двух заданных чисел. |
| Шаг 2: | Нахождение всех делителей выбранного наименьшего числа. |
| Шаг 3: | Проверка, являются ли найденные делители также делителями для второго числа. |
| Шаг 4: | Поиск наибольшего общего делителя из найденных общих делителей или установление, что НОД равен 1 (если общих делителей не найдено). |
Расчет НОД двух чисел является процедурой, основанной на простых математических операциях. Понимание этого процесса позволяет проводить различные анализы и решать задачи, связанные с доказательством взаимной простоты чисел, определением общих делителей и многим другим.
Алгоритм Евклида: нахождение наибольшего общего делителя
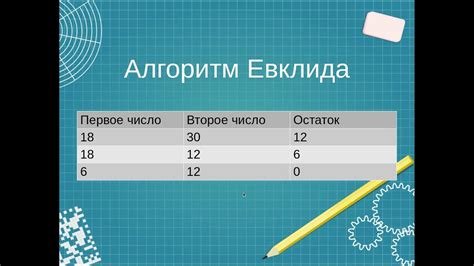
Алгоритм Евклида основывается на принципе, что для нахождения НОД двух чисел можно последовательно проводить деление одного числа на другое с вычислением остатка. Итерации алгоритма продолжаются до тех пор, пока остаток от деления не станет равным нулю. В этот момент последнее ненулевое число будет являться НОДом искомых чисел.
При использовании алгоритма Евклида для нахождения НОД чисел 455 и 968 мы последовательно делим большее число на меньшее число и вычисляем остаток от деления. Полученный остаток заменяет большее число, а меньшее число заменяется остатком. Этот процесс повторяется до тех пор, пока остаток от деления не станет равным нулю. На последней итерации полученное ненулевое число, которое заменило остаток, будет являться НОДом чисел 455 и 968.
Таким образом, алгоритм Евклида позволяет эффективно определить НОД двух чисел и является одним из важных инструментов для доказательства взаимной простоты чисел.
Алгоритмы проверки взаимной простоты
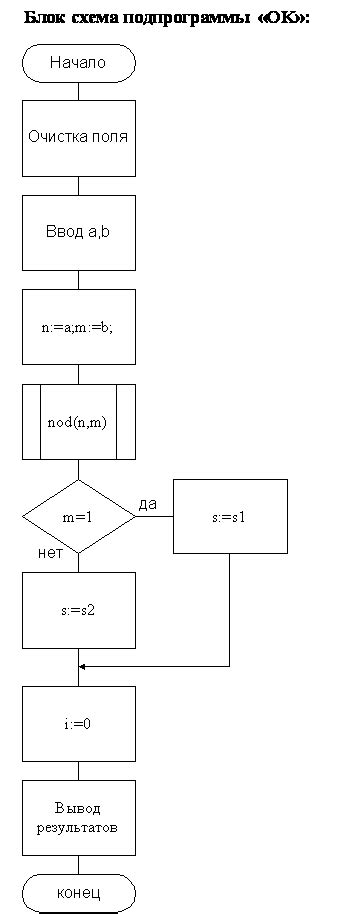
Первым методом является проверка наличия общих делителей у данных чисел. В случае если общих делителей нет, можно с уверенностью сказать, что числа взаимно просты. Однако, для ускорения процесса, можно применить более оптимальные алгоритмы.
Следующий алгоритм основан на использовании алгоритма Евклида для нахождения наибольшего общего делителя. Если НОД чисел равен 1, то это говорит о том, что числа являются взаимно простыми. Этот метод является достаточно эффективным, так как позволяет сократить количество операций.
Кроме того, существуют также вероятностные алгоритмы проверки взаимной простоты чисел, основанные на применении теории чисел и теста Рабина-Миллера. Они позволяют с большой вероятностью определить взаимную простоту чисел, хотя не дают абсолютно точного результата.
Итак, в данном разделе мы рассмотрели несколько алгоритмов проверки взаимной простоты чисел. Независимо от выбранного метода, важно учитывать эффективность и точность алгоритма, чтобы быстро и правильно определить, являются ли числа взаимно простыми.
Применение методов и алгоритмов к числам 455 и 968

В данном разделе рассмотрим применение различных методов и алгоритмов к числам 455 и 968, которые помогут нам установить их взаимную простоту. Мы изучим разные подходы, основанные на математических принципах, а также сравним эти числа с другими примерами для лучшего понимания.
Первым рассмотренным методом будет метод простого деления, который позволяет нам проверить, делится ли число на другое без остатка. Затем мы рассмотрим алгоритм Эвклида, который используется для нахождения наибольшего общего делителя двух чисел. Также мы изучим методы вычисления простых чисел и применим их к числам 455 и 968 для определения их простоты.
Далее мы рассмотрим метод факторизации чисел, который позволяет представить число в виде произведения простых множителей. Этот метод особенно полезен при проверке простоты чисел. Мы также обсудим алгоритмы поиска простых чисел и их применение при анализе чисел 455 и 968.
Кроме того, мы изучим методы проверки простоты чисел с помощью тестов на простоту, таких как тест Миллера-Рабина и тест Ферма. Проведем сравнительный анализ этих тестов и применим их к числам 455 и 968 для определения их простоты.
Исследование взаимной непростоты чисел 455 и 968

Раздел данной статьи посвящен изучению свойств чисел 455 и 968 с целью подтверждения их взаимной непростоты. Будут рассмотрены различные подходы и методы, позволяющие доказать отсутствие общих делителей у данных чисел.
Одним из методов, используемых для исследования взаимной непростоты чисел, является анализ их разложения на простые множители. Рассмотрение канонического разложения числа 455 и числа 968 поможет обнаружить наличие или отсутствие общих простых делителей.
| Число | Каноническое разложение |
|---|---|
| 455 | 5 * 7 * 13 |
| 968 | 2^3 * 11 * 11 |
Из разложения числа 455 видно, что оно содержит простые множители 5, 7 и 13. В то же время, разложение числа 968 представляет собой произведение простых множителей 2, 11 и 11. Поиск общих делителей между этими числами позволяет утверждать, что они не являются взаимнопростыми.
Кроме разложения на простые множители, в данном разделе рассматривается метод Евклида, основанный на алгоритме нахождения наибольшего общего делителя двух чисел. Применение этого метода к числам 455 и 968 также помогает подтвердить их взаимную непростоту.
Вопрос-ответ

Какие методы и алгоритмы используются для доказательства взаимной простоты чисел 455 и 968?
Для доказательства взаимной простоты чисел 455 и 968 можно использовать методы, основанные на факторизации чисел и нахождении их наибольшего общего делителя. Один из таких методов - алгоритм Евклида, который позволяет эффективно находить наибольший общий делитель. Также можно применить алгоритмы факторизации чисел на простые множители, такие как метод факторизации Ферма или метод квадратичного решета. В результате применения этих методов можно получить доказательство взаимной простоты чисел 455 и 968.
Какой алгоритм доказывает взаимную простоту чисел 455 и 968 надежно и быстро?
Для надежного и быстрого доказательства взаимной простоты чисел 455 и 968 можно использовать алгоритм Евклида. Этот алгоритм основан на поиске наибольшего общего делителя двух чисел. В данном случае, если наибольший общий делитель чисел 455 и 968 равен 1, то это говорит о их взаимной простоте. Алгоритм Евклида позволяет находить наибольший общий делитель эффективно и быстро, поэтому он подходит для данной задачи.
Возможно ли доказать взаимную простоту чисел 455 и 968 без использования алгоритма Евклида?
Да, возможно. Кроме алгоритма Евклида, существуют и другие методы и алгоритмы, которые позволяют доказать взаимную простоту чисел. Например, можно воспользоваться алгоритмами факторизации чисел на простые множители, такими как метод факторизации Ферма или метод квадратичного решета. Эти методы позволяют разложить числа на их простые множители и проверить, есть ли у них общие простые множители. Если общих простых множителей нет, то это говорит о взаимной простоте чисел 455 и 968.
Зачем нужно доказывать взаимную простоту чисел?
Доказательство взаимной простоты чисел позволяет нам установить, являются ли эти числа взаимно простыми или имеют общие делители. Это может быть полезно, например, при решении задач по теории чисел, шифровании данных или поиске наибольшего общего делителя.



