Древняя наука математики хранит в себе непомерный багаж знаний и секретов. Одним из сложнейших понятий, требующих особого внимания и понимания, является процесс нахождения производной функции. И если вас, уважаемые читатели, одержимо манит губительный разум математики, то смело отправляйтесь в путешествие по этапам дифференцирования вместе с нами.
Наши устремленные умы встретятся с великими уравнениями, представленными непостижимыми символами и знаками. Едва осознавая сущность своего стартового задания, должным образом продолжим наше исследование, чтобы обрести ключ к производной, это неуловимое комплексное число, воплощение интеграла значения, открытого в глубинах абстрактного мира математики.
Вдохновлены бесконечным величием чисел, проверенных парадоксами, мы направим наше внимание на аксиомы дифференцирования. Хотя их произнесение требует приложения некоторого умственного усилия, полученные нами осознания станут твердым убеждением в высших математических областях нашей сознательной жизни.
Что такое производная функции и какую роль она играет?

Чтобы проиллюстрировать роль производной функции, рассмотрим пример. Предположим, у нас есть функция, описывающая перемещение объекта в зависимости от времени. В таком случае, производная функции позволяет нам определить скорость перемещения объекта в каждый момент времени. Это может быть полезно для понимания, насколько быстро объект движется в определенный момент времени и для предсказания его будущего положения.
Таким образом, производная функции является важным инструментом в математике и ее применениях. Она позволяет анализировать и предсказывать изменения величин, а также определять их скорости изменения в конкретные моменты времени или точки. Понимание производной функции позволяет строить более точные модели и прогнозы, что делает ее неотъемлемой частью математического и научного подходов.
Определение производной

В данном разделе мы рассмотрим основное понятие, которое играет важную роль при изучении производных функций. Под определением производной понимается...
Для более наглядного представления определения производной, можно привести следующий пример:...
- Производная функции является мерой изменения значения функции по отношению к ее аргументу.
- Определение производной позволяет описать скорость изменения функции в каждой точке ее определения.
- Производная функции обладает важными геометрическими свойствами, такими как наклон касательной к графику функции.
- Различные функции могут иметь разные виды производных, такие как положительные, отрицательные, нулевые значения производной.
В результате понимания определения производной мы можем приступить к его применению для решения различных задач, связанных с анализом изменения функций и определением их экстремумов.
Сущность скорости изменения функции

Для лучшего понимания понятия скорости изменения функции, рассмотрим аналогию с движением. Когда мы говорим о скорости движения объекта, мы оцениваем, насколько быстро объект перемещается по пространству за определенный промежуток времени. Аналогично в функциях, скорость изменения определяет, насколько быстро функция меняется по отношению к изменению ее аргумента.
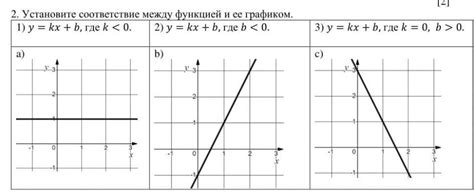
Представим себе график функции, где по горизонтальной оси отложены входные параметры, а по вертикальной оси – значения функции. В каждой точке графика существует наклон, который отражает скорость изменения функции в данной точке. Если наклон положительный, то функция увеличивается с ростом параметра; если наклон отрицательный, то функция уменьшается; а нулевой наклон указывает на то, что функция не меняется в данной точке.
| Наклон | Интерпретация |
|---|---|
| Положительный | Функция увеличивается с ростом аргумента |
| Отрицательный | Функция уменьшается с ростом аргумента |
| Нулевой | Функция не меняется в данной точке |
Понимание сущности скорости изменения функции является важным предшествующим шагом к пониманию процесса нахождения производной. Используя концепцию скорости изменения, мы сможем более глубоко и точно анализировать поведение функций, идентифицировать точки экстремума и строить более эффективные модели.
Примеры вычисления производной

Продемонстрируем простые примеры, как вычислить производную функции.
Производная функции – это ее изменение по отношению к аргументу. В других словах, это скорость изменения значения функции при изменении аргумента. Рассмотрим несколько примеров, чтобы лучше понять, как это работает.
Начнем с примера простой функции y = x^2. Для нахождения производной этой функции используем правило степенной функции: производная степенной функции равна произведению степени на коэффициент. В данном случае, производная функции y = x^2 будет равна 2x.
Далее рассмотрим более сложную функцию y = e^x. Для нахождения производной этой функции используем правило производной экспоненциальной функции: производная экспоненциальной функции равна самой функции, умноженной на производную основания экспоненты, то есть dy/dx(e^x) = e^x.
Еще один пример – функция y = ln(x). Для нахождения производной этой функции используем правило производной логарифмической функции: производная логарифмической функции равна 1/x, то есть dy/dx(ln(x)) = 1/x.
Это лишь несколько примеров из множества возможных функций, для которых можно найти производную. Правила и методы нахождения производной различных функций могут отличаться, но общая идея остается неизменной – производная функции показывает, как ее значение меняется при изменении аргумента. Умение находить производные позволяет анализировать и предсказывать поведение функций в различных ситуациях.
Прямая и косвенная взаимосвязь между функцией и временем
В данном разделе мы рассмотрим важную характеристику функций, а именно их зависимость от времени. Остроумно отражая изменения величин и явлений, время играет ключевую роль в определении поведения функций. Мы исследуем как функции прямо, так и косвенно зависят от временных факторов, а также рассмотрим, как эта зависимость повлияет на производную функции и ее свойства.
- Прямая зависимость от времени:
- Изменение функциональной зависимости в прямом соответствии с временем.
- Примеры прямой зависимости функции от времени.
- Влияние прямой зависимости на динамику функции и ее производную.
- Косвенная зависимость от времени:
- Изменение функциональной зависимости не в прямом соответствии с временем.
- Примеры косвенной зависимости функции от времени.
- Влияние косвенной зависимости на динамику функции и ее производную.
Изучение прямой и косвенной зависимости функций от времени поможет нам лучше понять, как изменения во времени влияют на их поведение и на различные свойства, такие как производные. Это важная концепция в математике и имеет широкое применение в различных областях науки и техники.
Методы нахождения производной функции

- Метод дифференцирования по определению
- Метод дифференцирования сложной функции
- Метод дифференцирования продукта
- Метод дифференцирования частного
Этот метод основан на определении производной функции через предел разности функции в точках. Суть метода заключается в том, чтобы вычислить предел отношения разности значений функции в двух близких точках к их разности аргументов при стремлении расстояния между точками к нулю.
Этот метод позволяет находить производную сложной функции, состоящей из нескольких простых функций, применяя цепное правило дифференцирования. Для применения метода необходимо использовать свойства производной, а именно правила дифференцирования сложной функции и правила дифференцирования элементарных функций.
Данный метод позволяет находить производную произведения двух функций по формуле дифференцирования произведения. Суть метода заключается в применении правила дифференцирования произведения, согласно которому производная произведения равна произведению производных функций и слагаемых.
Этот метод позволяет находить производную отношения двух функций по формуле дифференцирования частного. Для применения метода необходимо использовать правило дифференцирования частного, которое утверждает, что производная частного равна разности производных числителя и знаменателя, поделенной на квадрат знаменателя.
Выбор конкретного метода нахождения производной функции зависит от типа и структуры функции, а также от поставленной задачи. Знание различных методов дает возможность более гибко подходить к решению задач производной функции и эффективно применять их в практических ситуациях.
Метод дифференцирования по определению

В данном разделе мы рассмотрим метод дифференцирования по определению, который позволяет найти производную функции в конкретной точке. Применение этого метода требует аккуратного и последовательного выполнения шагов, чтобы получить точные результаты.
Дифференцирование по определению основано на концепции приближенного подсчёта скорости изменения функции в заданной точке. Мы выбираем точку, в которой хотим найти производную, и используем пределы для описания этой скорости изменения в момент времени или определённой точке.
Чтобы применить метод дифференцирования по определению, мы должны определить функцию, производную которой хотим найти, и выбрать точку, в которой хотим вычислить производную. Затем мы начинаем приближать рассмотрение двух очень близких точек на графике функции и вычисляем разделённую разность между значениями функции в этих точках. После этого мы уменьшаем расстояние между этими точками, чтобы увеличить точность приближения и получить более точное значение производной.
Метод дифференцирования по определению требует тщательных вычислений и применения пределов, чтобы получить точные результаты. Однако он является универсальным и может быть использован для любой функции, не зависимо от её сложности. Этот метод дает понимание о скорости изменения функции и позволяет нам найти тангенциальную линию к графику функции в заданной точке.
Операции дифференцирования базовых функций

Когда мы говорим о дифференцировании базовых функций, мы имеем в виду процесс нахождения производной функции, которая представляет собой мгновенную скорость изменения функции в каждой точке. Производная функции показывает, как изменяется значение функции при изменении аргумента.
В данном разделе мы рассмотрим операции дифференцирования, такие как дифференцирование константы, дифференцирование переменной, дифференцирование суммы и разности функций, дифференцирование произведения и частного функций, а также дифференцирование сложной функции.
При дифференцировании константы, производная всегда равна нулю, так как константа не меняется.
Дифференцирование переменной представляет собой нахождение производной по отношению к этой переменной. Например, если у нас есть функция f(x) = x, то ее производная будет равна единице, так как значение функции увеличивается одинаково с изменением аргумента.
Дифференцирование суммы и разности функций выполняется путем дифференцирования каждой функции по отдельности и сложения или вычитания их производных.
Дифференцирование произведения и частного функций выполняется с помощью правила производной произведения и правила производной частного соответственно.
Для дифференцирования сложной функции, мы используем правило дифференцирования сложной функции, которое позволяет выразить производную сложной функции через производные внутренней и внешней функций.
В данном разделе будут представлены примеры применения этих операций дифференцирования к базовым функциям, чтобы помочь вам лучше понять процесс нахождения производной функции.
Применение правила дифференцирования сложной функции

Важным инструментом при дифференцировании сложной функции является правило дифференцирования сложной функции, также называемое правилом цепной производной. Это правило позволяет найти производную сложной функции, используя производные внутренних и внешних функций, связанных между собой.
Применение правила дифференцирования сложной функции состоит из двух основных шагов. Вначале необходимо найти производную внутренней функции, затем производную внешней функции. Результатом будет произведение этих двух производных.
Для наглядного объяснения применения правила дифференцирования сложной функции, рассмотрим пример: функция y = (3x^2 + 2x - 1)^4. Сначала мы найдем производную внутренней функции, которой является выражение 3x^2 + 2x - 1. Затем найдем производную внешней функции, возведя внутреннюю функцию в степень 4. Полученные производные умножим друг на друга, и наша итоговая производная будет:
- Производная внутренней функции: dy/dx = 6x + 2
- Производная внешней функции: d(u^n)/dx = 4(u^(n-1))*du/dx = 4(3x^2 + 2x - 1)^3*(6x + 2)
- Итоговая производная: dy/dx = (6x + 2)*(4(3x^2 + 2x - 1)^3)
Таким образом, мы успешно применили правило дифференцирования сложной функции и нашли производную исходной функции y = (3x^2 + 2x - 1)^4.
Вопрос-ответ

Каким образом можно найти производную функции?
Производную функции можно найти с помощью правил дифференцирования, таких как правило дифференцирования суммы, правило дифференцирования произведения, правило дифференцирования сложной функции и других. Необходимо найти производную каждого слагаемого или множителя и объединить результаты согласно соответствующему правилу. Также можно использовать таблицу производных, в которой представлены производные основных функций.
Можете привести пример нахождения производной функции?
Конечно! Давайте рассмотрим функцию f(x) = 3x^2 + 2x + 1. Для нахождения производной этой функции, нужно поочередно дифференцировать каждое слагаемое. Производная от 3x^2 равна 6x (так как 3 умножается на 2, а x возводится в степень 2, затем показатель степени умножается на коэффициент перед x). Производная от 2x равна 2 (так как 2 умножается на 1, а x возводится в степень 1). Производная от 1 равна 0 (так как константа дифференцируется как 0). Итак, производная функции f(x) равна 6x + 2.
Есть ли особые случаи в поиске производной функции?
Да, есть несколько особых случаев, с которыми нужно быть осторожными. Например, для константной функции (функция, которая не зависит от переменной) производная равна 0. Также, для функции, в которой переменная возводится в степень 0, производная также равна 0. Если функция имеет разрывы или точки разрыва, нужно учитывать особенности в этих точках при нахождении производной.
Как можно найти производную сложной функции?
Для нахождения производной сложной функции можно использовать правило дифференцирования сложной функции, которое называется правилом цепной дифференциации. Нужно найти производную внешней функции и производную внутренней функции, а затем перемножить их. Например, для функции f(x) = sin(x^2) мы сначала дифференцируем внутреннюю функцию, получаем f'(x) = 2x, а затем дифференцируем синус от полученного результата, получаем f'(x) = 2x*cos(x^2).
Что такое производная функции?
Производная функции - это показатель скорости изменения функции в каждой ее точке. В более простых словах, это показывает, насколько быстро значение функции меняется при изменении ее входного параметра.
Зачем нужно находить производную функции?
Нахождение производной функции имеет много практических приложений. Например, оно позволяет найти экстремумы функции (точки минимума или максимума), а также определить, в какую сторону и как быстро изменяется значение функции в каждой ее точке.