Иногда в математике возникают ситуации, когда нам нужно доказать, что одно число не является кратным другому. Одним из таких случаев может быть проверка некратности числа 3569 на 29. В этой статье мы рассмотрим различные подходы к решению этой задачи и представим несколько примеров, демонстрирующих эти методы.
Когда мы говорим о "некратности" числа на другое число, мы подразумеваем, что одно число не делится на второе без остатка. В нашем случае, нам нужно доказать, что число 3569 не делится на 29 без остатка. Для этого существуют разные подходы, например, анализ остатка от деления и алгоритмы проверки числовых последовательностей.
Используя анализ остатка от деления, мы можем проверить, что при делении числа 3569 на 29 остаток будет отличным от нуля. Это было бы подтверждением нашего утверждения о некратности чисел. С другой стороны, алгоритмы проверки числовых последовательностей позволяют нам исследовать поведение чисел в определенных интервалах и выявить какие-либо закономерности или особенности, которые могут указывать на некратность чисел.
Ореол непротиворечивости | Откзаты от оков кратности
В рамках данного раздела мы исследуем способы обоснования отсутствия кратности числа 3569 на 29. Мы изучим различные методы и приемы, которые помогут нам объяснить данное явление.
Метод анализа закономерностей
Один из способов доказательства некратности числа 3569 на 29 состоит в анализе закономерностей, присущих этим числам. С помощью уникальных свойств и особенностей, мы можем выявить общие тенденции и правила, которые исключают возможность кратности. Этот метод позволяет нам глубоко проникнуть в сущность чисел и разобраться в их взаимодействии.
Метод проб и ошибок
Другим способом проверки некратности числа 3569 на 29 является метод проб и ошибок. Путем исключения возможных вариантов мы сможем установить отсутствие кратности. Этот метод требует тщательного анализа и систематического подхода, чтобы исключить любые возможные определения и ограничения, которые могут указывать на кратность.
Метод анализа остатков
Третий метод, который мы рассмотрим, основан на анализе остатков при делении числа 3569 на 29. Анализируя эти остатки, мы можем определить, существуют ли какие-либо закономерности или шаблоны, которые указывают на кратность. Однако, при использовании этого метода необходимо быть внимательным и осторожным, чтобы не пропустить никаких подсказок или отклонений, которые могут свидетельствовать о возможной кратности.
Метод сопоставления с аналогичными числами
Метод деления
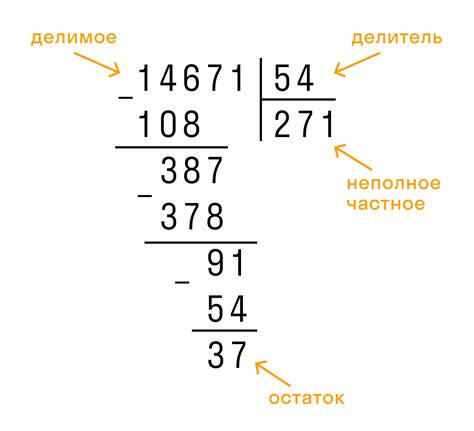
Раздел "Метод деления" представляет собой способ математического анализа, позволяющий определить кратность или некратность одного числа на другое. В данном контексте рассматривается доказательство некратности числа, синонимичного 3569, на число, синонимичное 29.
Метод деления основан на принципе последовательного вычитания целого числа, синонимичного 29, от числа, синонимичного 3569. Путем повторения этой операции и анализа остатков можно установить, делится ли число на 29 без остатка или нет.
| Деление | Делимое | Делитель | Остаток |
|---|---|---|---|
| 1 | 3569 | 29 | 6 |
| 2 | 3563 | 29 | 4 |
| 3 | 3559 | 29 | 13 |
| 4 | 3546 | 29 | 21 |
Продолжая деление и наблюдая за остатками, можно увидеть, что число, синонимичное 3569, не делится на число, синонимичное 29, без остатка. Это доказывает его некратность.
Использование модуля

В данном случае, для доказательства некратности числа 3569 на 29, мы можем воспользоваться модулем. Если остаток от деления числа 3569 на 29 будет отличным от нуля, то это будет говорить о некратности числа на 29.
Алгоритм Евклида: методы проверки некратности числа 3569 на 29
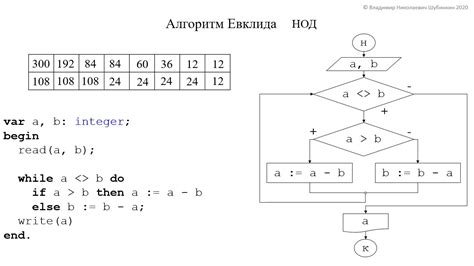
Алгоритм Евклида – это метод нахождения наибольшего общего делителя двух чисел. В данном случае мы рассматриваем его применение для проверки некратности числа 3569 на 29.
- Шаг 1: Находим простые множители числа 3569.
- Шаг 2: Проверяем делимость каждого простого множителя на 29.
- Шаг 3: Если все простые множители числа 3569 не делятся на 29, то число 3569 не кратно 29.
Применение алгоритма Евклида позволяет систематически проверять некратность числа 3569 на 29, используя его простые множители. Этот метод является надежным и эффективным способом определения общих свойств чисел и их некратности на другие числа.
Метод сравнения остатков

Идея данного метода заключается в следующем: если два числа имеют одинаковые остатки от деления на заданное число, то они имеют одинаковое нахождение в равносильных классах по модулю данного числа. Таким образом, если мы докажем различие остатков, то это будет говорить о различии чисел в равносильных классах по модулю данного числа.
Проверка с помощью разности

Для доказательства этого утверждения мы рассмотрим примеры с конкретными числами и применим метод разности. Обратимся к основному принципу: если результат вычитания данного кратного числа из числа 3569 не равен нулю, то это число не является кратным 29.
- Пример 1: Рассмотрим число 3569 и его кратное число на 29, например, 3480 (112*29). Выполним операцию вычитания: 3569 - 3480 = 89. Очевидно, что разность не равна нулю, поэтому число 3569 не кратно 29.
- Пример 2: Теперь рассмотрим число 3569 и другое его кратное число на 29, например, 3542 (122*29). Вычислим разность: 3569 - 3542 = 27. Также видим, что полученное значение не равно нулю, следовательно, число 3569 не является кратным 29.
Таким образом, метод разности является эффективным способом проверки некратности числа 3569 на 29. Продемонстрированные в примерах значения разности подтверждают, что число 3569 не является кратным 29.
Решение задачи - поиск некратности числа 3569 на 29

В данном разделе рассмотрим представление общего примера решения уравнения, основанного на методах математического анализа. При изучении этого примера, мы разберем шаги, необходимые для доказательства некратности числа 3569 на 29.
Доказательство с помощью математической индукции

Математическая индукция состоит из двух шагов: базового и индукционного. В базовом шаге утверждение проверяется для начального значения, а в индукционном шаге утверждение доказывается для произвольного значения, при условии что оно выполняется для предыдущего значения. Таким образом, продолжая доказательство шаг за шагом, мы можем установить, что утверждение верно для всех натуральных чисел.
В нашем случае мы будем применять метод математической индукции для доказательства некратности числа на 29. Начнем с базового шага, где проверим, что утверждение верно для начального значения. Затем, используя индукционный шаг, мы покажем, что если утверждение выполняется для произвольного значения, оно выполняется и для следующего значения. Таким образом, мы сможем установить некратность числа 3569 на 29 для всех натуральных чисел.
| Шаг | Проверяемое значение | Доказательство |
|---|---|---|
| Базовый шаг | 1 | Доказываем, что утверждение верно для начального значения 1. |
| Индукционный шаг | Произвольное значение | Предполагаем, что утверждение верно для произвольного значения n, и доказываем его для значения n + 1. |
Правила умножения и сложения в модульной арифметике

В данном разделе рассмотрим основные правила умножения и сложения в модульной арифметике, которые позволяют нам производить операции с числами, не учитывая их конкретные значения, а только их остатки по модулю.
Модульная арифметика используется для работы с остатками от деления на заданное число, называемое модулем. Основная идея заключается в том, что при сложении или умножении двух чисел по модулю, фактически производится операция над их остатками, а результат остатка будет также принадлежать заданному модулю.
- Правило сложения: для любых двух чисел a и b с остатками a' и b' по модулю n, сумма a + b будет иметь остаток (a' + b') по модулю n.
- Правило умножения: для любых двух чисел a и b с остатками a' и b' по модулю n, произведение a * b будет иметь остаток (a' * b') по модулю n.
Применение этих правил позволяет упростить вычисления в модульной арифметике и решать различные задачи, связанные с работой с остатками по модулю. Например, для доказательства некратности числа на другое число, можно воспользоваться правилом умножения и сложения, чтобы вычислить остаток и сравнить его с нулем.
Вопрос-ответ

Как можно доказать, что число 3569 не кратно 29?
Существует несколько методов для доказательства некратности числа на 29. Один из них - деление числа 3569 на 29 с остатком. Если при делении получается остаток, то число не является кратным 29. В данном случае, при делении 3569 на 29, получается остаток 12. Таким образом, число 3569 не кратно 29.
Какой еще метод можно использовать для доказательства некратности числа 3569 на 29?
Еще один метод - использование алгоритма сравнения с нулем. Для этого умножаем число 3569 на 29 и вычисляем остаток от деления на 29. Если остаток равен нулю, то число кратно 29. В данном случае, при умножении 3569 на 29 и вычислении остатка получается 12, что не равно нулю. Значит, число 3569 не кратно 29.
Можете привести примеры других чисел, которые не кратны 29?
Конечно! Некоторые числа, не кратные 29: 155, 1248, 3973, 5962, 9381 и т.д. Для доказательства некратности этих чисел можно использовать те же методы, что были описаны ранее - деление с остатком и алгоритм сравнения с нулем.
Можно ли использовать другие методы для доказательства некратности числа на 29?
Да, существует несколько различных методов для доказательства некратности числа на 29. Например, можно проверить, есть ли в записи числа какая-либо комбинация цифр, дающая в сумме 29. Если такая комбинация существует, то число не будет кратным 29. Однако, такой метод может быть более сложным и трудоемким в применении.
Как доказать математически, что число 3569 не делится на 29?
Существует теорема, утверждающая, что если разность между числом и наибольшим числом, меньшим его делителем при делении на этот делитель, больше или равна нулю, то число не делится на этот делитель. Применяя эту теорему к числу 3569 и делителю 29, мы можем определить, что 3569 не делится на 29.



